Digital Electronics : Number System

Number system

Introduction

The System which is used to represent the numbers is called as number system. In Digital systems, there are different types of number system which would be used for the representation of the information. The machine understandable binary system is also one of them. There are different types of number systems based on their base/radix. Base or radix of the number system is the total number of symbols used in that number system. 

For example, Decimal will have 10 symbols as 0,1,......9.

Types of Number system

Below are the most common types of the number systems which are used in the digital electronics.

• Decimal
• Binary
• Octal
• Hexa-Decimal

Decimal

The numbers in the decimal number system has a base/radix of 10. The symbols in the decimal number systems are 0,1,2,3,4,5,6,7,8 and 9. This is the number system which we are using in or daily life. Each position in the number system will represent the power of "10".

For example,

(1987)₁₀ => (7 x 10⁰) + (8 x 10¹) + (9 x 10²) + (1 x 10³)

Binary

The numbers in the binary number system has a base/radix of 2. The symbols in the binary number systems are 0 and 1. This is the number system which is used in the digital systems. Each position in the number system will represent the power of "2".

For example,

(1011)₂ => (1 x 2⁰) + (1 x 2¹) + (0 x 2²) + (1 x 2³) => (11)₁₀

Octal

The numbers in the octal number system has a base/radix of 8. The symbols in the octal number systems are 0,1,2,3,4,5,6 and 7. Each position in the number system will represent the power of "8".

3 Bits are required to represent the number in the each position of octal number system.

For example,

(7024)8 => (4 x 8⁰) + (2 x 8¹) + (0 x 8²) + (7 x 8³) => (3604)₁₀

Hexa-Decimal

The numbers in the Hexa-decimal number system has a base/radix of 16. The symbols in the hexa-decimal number systems are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F. Each position in the number system will represent the power of "16".

4 Bits are enough to represent the number in the hexa decimal number system.

For example,

(7A24)16 => (4 x 16⁰) + (2 x 16¹) + (A x 16²) + (7 x 16³) => (31268)₁₀

_Conversion

Any number system To Decimal

To convert any number system to decimal number system,

(A3A2A1A0)_n => [(A0 x n⁰) + (A1 x n¹) + (A2 x n²) + (A3 x n³)]₁₀

_Example,

Binary to Decimal           : (1011)₂       => (1 x 2⁰) + (1 x 2¹) + (0 x 2²) + (1 x 2³) => (11)₁₀

Octal to Decimal             : (7024)8       => (4 x 8⁰) + (2 x 8¹) + (0 x 8²) + (7 x 8³) => (3604)₁₀

Hexa-Decimal to Binary : (7A24)16     => (4 x 16⁰) + (2 x 16¹) + (A x 16²) + (7 x 16³) => (31268)₁₀

Decimal to Any number system

Decimal to Binary

Procedure to convert the decimal number into binary,

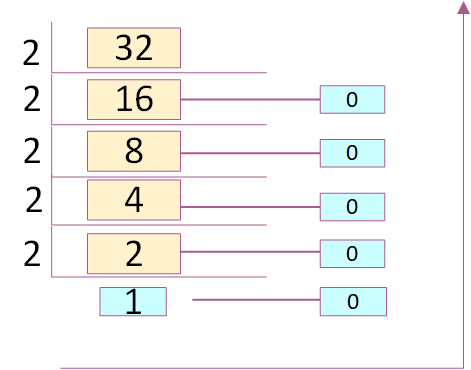
Step 1: Divide the given decimal number by "2".

Step 2: Keep both remainder and quotient.

Step 3: Repeat step1 and 2, until you get "1" as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required binary number will be obtained.

Example,

(32)₁₀ => Binary

(32)₁₀ => (100000)₂

Decimal to Octal

Procedure to convert the decimal number into Octal,

Step 1: Divide the given decimal number by "8".

Step 2: Keep both remainder and quotient.

Step 3: Repeat step1 and 2, until you get  1,2,3,4,5,6 or 7 as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required octal number will be obtained.

Example,

(64)₁₀ => Octal

(64)₁₀ => (100)₈

Decimal to Hexa-Decimal

Procedure to convert the decimal number into Hexa-Decimal,

Step 1: Divide the given decimal number by "16".

Step 2: Keep both remainder[in the form of hexa-decimal] and quotient.

Step 3: Repeat step1 and 2, until you get  1,2,3,4,5,6,7,8,9,A,B,C,D or E as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required octal number will be obtained.

Example,

(64)₁₀ => Hexa-decimal

(64)₁₀ => (4F)₁₆

Binary to Octal/Hexa-Decimal

Binary to Octal

3 Bits are required to represent the number in the each position of octal number system. So we can simply convert binary to octal by collating each 3 bits starting from LSB.

Example,

(1110101110001)2 => 

                            (1 110 101 110 001)2 = (16561)8

Binary to Hexa-Decimal

4 Bits are required to represent the number in the each position of hexa-decimal number system. So we can simply convert binary to hexa-decimal by collating each 4 bits starting from LSB.

Example,

(1110101110001)2 => 

                            (1 1101 0111 0001)2 = (1D71)16

Octal/Hexa-Decimal to Binary

Octal to Binary

We could simply convert each digit in the octal number to 3 bits[binary].

Example,

(16561)8 => 

                            (16561)8 =  (001 110 101 110 001)2

Binary to Hexa-Decimal

We could simply convert each digit in the hexa-decimal number to 4 bits[binary].

Example,

(1D71)16 => 

                             (1D71)16 = (0001 1101 0111 0001)2

Conversion Table