Digital Electonics

Number system

Introduction
The System which is used to represent the numbers is called as number system. In Digital systems, there are different types of number system which would be used for the representation of the information. The machine understandable binary system is also one of them. There are different types of number systems based on their base/radix. Base or radix of the number system is the total number of symbols used in that number system. 
For example, Decimal will have 10 symbols as 0,1,......9.

Types of Number system
Below are the most common types of the number systems which are used in the digital electronics.
  • Decimal
  • Binary
  • Octal
  • Hexa-Decimal

Decimal

The numbers in the decimal number system has a base/radix of 10. The symbols in the decimal number systems are 0,1,2,3,4,5,6,7,8 and 9. This is the number system which we are using in or daily life. Each position in the number system will represent the power of "10".

For example,
(1987)10 => (7 x 100) + (8 x 101) + (9 x 102) + (1 x 103)

Binary

The numbers in the binary number system has a base/radix of 2. The symbols in the binary number systems are 0 and 1. This is the number system which is used in the digital systems. Each position in the number system will represent the power of "2".

For example,
(1011)2 => (1 x 20) + (1 x 21) + (0 x 22) + (1 x 23) => (11)10

Octal

The numbers in the octal number system has a base/radix of 8. The symbols in the octal number systems are 0,1,2,3,4,5,6 and 7. Each position in the number system will represent the power of "8".
3 Bits are required to represent the number in the each position of octal number system.

For example,
(7024)8 => (4 x 80) + (2 x 81) + (0 x 82) + (7 x 83) => (3604)10

Hexa-Decimal

The numbers in the Hexa-decimal number system has a base/radix of 16. The symbols in the hexa-decimal number systems are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E and F. Each position in the number system will represent the power of "16".
4 Bits are enough to represent the number in the hexa decimal number system.

For example,
(7A24)16 => (4 x 160) + (2 x 161) + (A x 162) + (7 x 163) => (31268)10

Conversion

Any number system To Decimal

To convert any number system to decimal number system,

(A3A2A1A0)n => [(A0 x n0) + (A1 x n1) + (A2 x n2) + (A3 x n3)]10

Example,

Binary to Decimal           : (1011)2       => (1 x 20) + (1 x 21) + (0 x 22) + (1 x 23) => (11)10
Octal to Decimal             : (7024)8       => (4 x 80) + (2 x 81) + (0 x 82) + (7 x 83) => (3604)10
Hexa-Decimal to Binary : (7A24)16     => (4 x 160) + (2 x 161) + (A x 162) + (7 x 163) => (31268)10

Decimal to Any number system

Decimal to Binary

Procedure to convert the decimal number into binary,

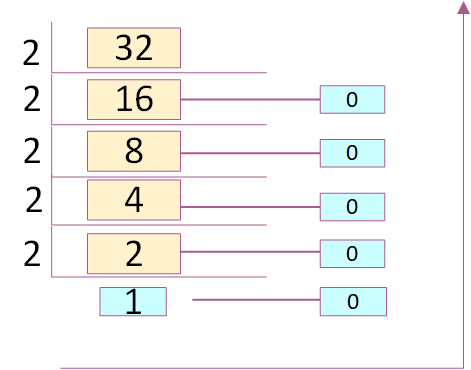
Step 1: Divide the given decimal number by "2".

Step 2: Keep both remainder and quotient.

Step 3: Repeat step1 and 2, until you get "1" as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required binary number will be obtained.

Example,

(32)10 => Binary

(32)10 => (100000)2

Decimal to Octal

Procedure to convert the decimal number into Octal,

Step 1: Divide the given decimal number by "8".

Step 2: Keep both remainder and quotient.

Step 3: Repeat step1 and 2, until you get  1,2,3,4,5,6 or 7 as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required octal number will be obtained.

Example,

(64)10 => Octal

(64)10 => (100)8

Decimal to Hexa-Decimal

Procedure to convert the decimal number into Hexa-Decimal,

Step 1: Divide the given decimal number by "16".

Step 2: Keep both remainder[in the form of hexa-decimal] and quotient.

Step 3: Repeat step1 and 2, until you get  1,2,3,4,5,6,7,8,9,A,B,C,D or E as quotient.

Step 4 : Keeping last quotient as MSB and all the remainders in bottom to top order, the required octal number will be obtained.

Example,

(64)10 => Hexa-decimal

(64)10 => (4F)16

Binary to Octal/Hexa-Decimal

Binary to Octal

3 Bits are required to represent the number in the each position of octal number system. So we can simply convert binary to octal by collating each 3 bits starting from LSB.

Example,

(1110101110001)2 => 
                            (1 110 101 110 001)2 = (16561)8

Binary to Hexa-Decimal

4 Bits are required to represent the number in the each position of hexa-decimal number system. So we can simply convert binary to hexa-decimal by collating each 4 bits starting from LSB.

Example,

(1110101110001)2 => 
                            (1 1101 0111 0001)2 = (1D71)16

Octal/Hexa-Decimal to Binary

Octal to Binary

We could simply convert each digit in the octal number to 3 bits[binary].

Example,

(16561)8 => 
                            (16561)8 =  (001 110 101 110 001)2

Binary to Hexa-Decimal

We could simply convert each digit in the hexa-decimal number to 4 bits[binary].

Example,

(1D71)16 => 
                             (1D71)16 = (0001 1101 0111 0001)2

Conversion Table


 Binary Number Representation

There are 2 different kind of  binary numbers representation.

Unsigned Binary

Unsigned number contains only magnitude of the number.

Representation of Unsigned Binary

8 Bit unsigned number will be used to represent 0 to +255.

(11100101)2 =>  (1 x 20) + (0 x 21) + (1 x 22) + (0 x 23) + (0 x 24) + (1 x 25) + (1 x 26) + (1 x 27)  

                    => (229)10

Signed Binary

Signed number contains both sign and magnitude of the number. MSB bit indicates the sign of the number.

Representation of  Signed Binary

There are 3 different kind of representation of Signed Binary numbers.

  1. Sign Bit Magnitude
  2. 1's complement
  3. 2's complement
Sign Bit Magnitude

In Sign-Bit Magnitude format, MSB bit will be the sign bit and other bits in the number will contribute to magnitude.
8 Bit Signed Bit magnitude number will be used to represent -127 to +127

(11100101)2 =>  (1 x 20) + (0 x 21) + (1 x 22) + (0 x 23) + (0 x 24) + (1 x 25) + (1 x 26)  

                    => (-101)10

(00000101)2 => (1 x 20) + (0 x 21) + (1 x 22) + (0 x 23) + (0 x 24) + (0 x 25) + (0 x 26) 

                    => (+5)10


1's Complement

For positive numbers  1's complement form will remain same as sign bit magnitude.
Only for negative numbers, all the bits including sign bit will get inverted.

8 Bit 1's complement number will be used to represent -127 to +127

(11100101)2 =>  00011010 => (0 x 20) + (1 x 21) + (0 x 22) + (1 x 23) + (1 x 24) + (0 x 25) + (0 x 26) + (0 x 27)  

                    => (-26)10

(00000101)2 => (1 x 20) + (0 x 21) + (1 x 22) + (0 x 23) + (0 x 24) + (0 x 25) + (0 x 26) + (0 x 27)  

                    => (+5)10

2's Complement

For positive numbers  2's complement form will remain same as sign bit magnitude.
Only for negative numbers, all the bits including sign bit will get inverted and get added with 1'b1.

8 bit signed binary number will be used to represent -128 to +127.

(11100101)2 =>  (1 x 20) + (0 x 21) + (1 x 22) + (0 x 23) + (0 x 24) + (1 x 25) + (1 x 26) + ((-1) x 27)  

                    => (-27)10

(00001101)2 => (1 x 20) + (0 x 21) + (1 x 22) + (1 x 23) + (0 x 24) + (0 x 25) + (0 x 26) + (0 x 27)  

                    => (+13)10

Representation Table


Logic Gates

AND Gate                                

Functionality

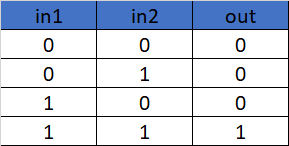
 It will output High[1] only if all the inputs to the gate are High[1]. If any of the inputs to the AND gate is Low, it will output Low[0]. The function can be extended to any number of inputs.

Symbol

Boolean Expression    

Truth Table

   

Implementation using Diode




OR Gate                                

Functionality

 It will output Low[0] only if all the inputs to the gate are Low[0]. If any of the inputs to the OR gate is High, it will output High[1]. The function can be extended to any number of inputs.

Symbol

Boolean Expression


Truth Table


Implementation using Diode


NOT Gate                                

Functionality

 It will invert the input being applied.

Symbol


Boolean Expression

Truth Table


NAND Gate                                

Functionality

It will output Low[0] only if all the inputs to the gate are High[1]. If any of the inputs to the AND gate is Low, it will output High[1]. Nand gate consists of  an AND gate followed by a NOT gate[inverter].

Symbol

Boolean Expression

Truth Table


NOR Gate                                

Functionality

 It will output High[1] only if all the inputs to the gate are Low[0]. If any of the inputs to the OR gate is High, it will output Low[0]. NOR gate consists of  an OR gate followed by a NOT gate[inverter].

Symbol

Boolean Expression

Truth Table


XOR Gate                                

Functionality

 It will output High[1]  if both the inputs are different, else will output Low[0].

Symbol

Boolean Expression

Truth Table


XNOR Gate                                

Functionality

 It will output High[1]  if both the inputs are same, else will output Low[0]. XNOR gate consists of a XOR gate followed by a NOT gate.

Symbol

Boolean Expression

Truth Table


Universal Gates

Nand and Nor gates are called as universal gates, as we could implement other basic gates[AND,OR,NOT] just by using nand or nor gates.

Basic Gates Implementation using NAND


1.NOT using NAND


As NOT gate have only 1 input and both not and nand have inverted version at the output, we could simply short 2 inputs of the NAND gate to make it behave as a NOT gate. 

Below is the implementation,

2.AND using NAND


If we look at the truth table of both the gates, we could clearly understand that the output of AND gate is just an inverted version of NAND gate's. So we can implement an AND gate by inverting the NAND gate's output. Since we have to implement the whole AND gate by NAND itself, we need an inverter also in the form of NAND gate.

Below is the implementation,

3.OR using NAND       


As per the De Morgan's theorem,



Hence, If we invert the inputs of the NAND gate output will be A + B.

Below is the implementation,


No comments:

Post a Comment

Subscribe to: Posts (Atom)

Digital Electronics - Binary Number Representation

  Binary Number Representation There are 2 different kind of  binary numbers representation. Unsigned Binary Unsigned number contains only m...

  • Digital Electronics - Logic Gates
    Logic Gates AND Gate                                   Functionality  It will output High[1] only if all the inputs to the gate are High[1]....